
はじめに
はじめまして、株式会社TechouseでエンジニアインターンをしているMatsu-Nobuです!
今回は、RubyKaigi 2025 1日目のmakenowjustさんによるセッション「Make Parsers Compatible Using Automata Learning」を聴講したので、その内容をブログにまとめていきます。
セッションの概要
はじめに、本セッションの概要を説明します。
Rubyには、parse.yからパーサージェネレータを使って生成したパーサーと、手書きパーサーであるPrismの2種類のパーサーが存在します。 本セッションでは、「オートマトン学習」という技術を用いてこれら2つのパーサーの間の互換性の問題を発見したことについて述べられました。 また、オートマトン学習のアルゴリズムの1つであるAngluinのL*や、その背景知識となるオートマトン理論の基礎についてもわかりやすく解説されました。
次章からは、セッションの各トピックについて詳細に述べていきます。
Rubyの2つのパーサー
Rubyには、2つのパーサー(構文解析器)が存在します。これらのパーサーは同じ言語仕様を実装していますが、アプローチや実装方法が異なります。
1つ目は、パーサージェネレータによって生成されたパーサーです。 Cで実装されたパーサージェネレータであるbisonを用いて、文法規則を記述したparse.yというファイルからパーサーが生成されます。 このパーサーは長年Rubyの標準パーサーとして使用されてきました。 最近ではLramaというパーサージェネレータに置き換えられましたが、基本的な考え方は同じです。
2つ目は、手書きパーサーであるPrismです。 PrismはCで実装されており、メモリ管理や実行速度の最適化が施されています。 また、ライブラリとして使いやすいAPIが提供されているため、外部ツールからも利用しやすいという特徴があります。
Rubyでは、--parserオプションを使用することで、これら2つのパーサーを切り替えることができます。また、RubyVM、Ripper、syntax_tree、parser gemなど、他にもRubyのコードを解析するためのツールが存在します。
パーサー間の互換性の問題
これらの異なるパーサー実装が存在することで、互換性の問題が生じる可能性があります。 特に、一方のパーサーでは正しく解析できるのに、もう一方では解析できないというケースが発生すると、あるパーサー実装では正常に動作するコードが、別のパーサー実装では動作しない状況となります。 こうした事態は開発者にとって重大な問題です。
このような互換性の問題を発見するためには、以下のようなアプローチが考えられます。
- 単体テスト: 特定の文法に対して各パーサーの動作を検証する
- 実際のgemをパースしてテスト: 実際のRubyのgemを2つのパーサーでパースして動作確認し、互換性をテストする
- ファジング: ランダムに生成されたコードを両方のパーサーに与えて挙動の違いを検出する
しかし、これらの方法はどれもいわゆる物量攻めのアプローチです。Rubyの複雑な構文全体をカバーするのは非常に困難で、全ての構文パターンを網羅的にチェックするには膨大な時間と労力が必要となります。
そこで、より形式的かつ効率的に互換性の問題を検証できないかという課題が生まれました。 オートマトン理論を応用することで、この問題に対する新しいアプローチが可能になります。
形式言語とオートマトン
オートマトン理論は、計算機科学の基礎となる理論の1つで、形式言語を認識するための数学的モデルを提供します。 オートマトンの一種である決定性有限オートマトン(DFA)は、以下の5つの組で定義されます:
- Q: 状態の有限集合
- Σ: アルファベット(記号の集合)
- q0: 初期状態
- F: 受理状態の集合
- δ: 遷移関数(現在の状態と入力アルファベットから次の状態を決定する関数)
オートマトンは、入力された文字列を一文字ずつ読み込みながら状態を遷移させていき、最終的に受理状態に達した場合、その文字列を受理します。 オートマトンによって受理される文字列の集合を、そのオートマトンが受理する言語と呼びます。
決定性有限オートマトンと正規表現は密接な関係があり、相互に変換可能です。 どちらも言語、すなわち文字列の集合を扱うための手段であり、特定のパターンに一致する文字列を表現するために使用されます。
本セッションでも例として挙げられた以下のDFAを使って、オートマトンの具体的な動作について説明します。
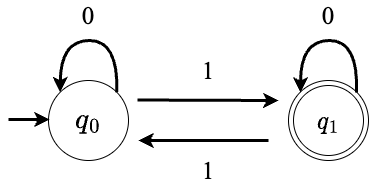
このDFAはq0, q1という2つの状態からなり、初期状態はq0、受理状態はq1です。
このDFAに010という文字列を入力する場合を考えます。
最初は初期状態であるq0にいて、1文字目の0を読み込み、遷移関数(矢印)に従ってq0に遷移します。
続いて、q0にいる状態で2文字目の1を読み込み、遷移関数に従ってq1に移動します。
最後に、q1にいる状態で3文字目の0を読み込み、遷移関数に従ってq0に移動します。
最終的に受理状態であるq1に達しているため、このDFAは文字列010を受理します。
このDFAを正規表現に変換すると、/0*1(0*10*1)*/となります。
このDFAが受理する言語と、正規表現/0*1(0*10*1)*/にマッチする文字列は一致します。
オートマトンの大きな利点は、受理する言語の集合演算を効率的に計算できることです。例えば以下のような演算が考えられます。
- 和集合(OR)
- 積集合(AND)
- 差集合
- 対称差集合 (XOR)
特に対称差の計算が重要で、これにより2つのオートマトンの「違い」を明確に特定することができます。
例えば、2つのオートマトンの受理する言語の積集合を計算するには、次のような手順で行います。 まず、2つのオートマトンを合成し、これらの動作を同時にシミュレーションするような1つのオートマトンを作ります。(この操作はオートマトンの並列合成と呼ばれます)
例を挙げて説明します。 以下のDFA A, Bを合成することを考えます。
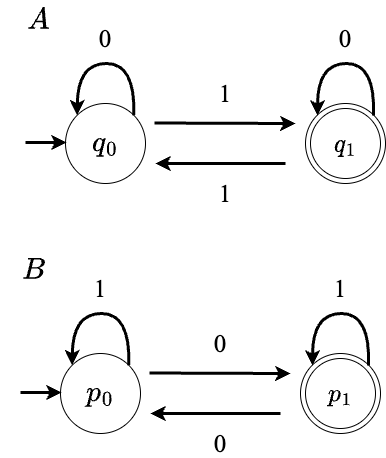
その場合、以下のように、合成したオートマトンの状態集合は2つのオートマトンの状態集合の直積とし、遷移関係は以下の図中の規則を満たすようにします。
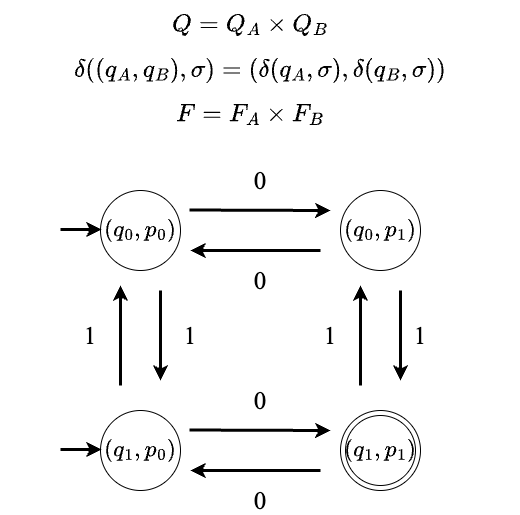
そして、合成したオートマトンの受理状態は、2つのオートマトンが同時に受理状態となる部分とします。こうして得られたオートマトンは、元の2つのオートマトンが受理する言語の積集合を受理するオートマトンとなります。 XOR演算の場合は、一方のみが受理状態になる部分を受理状態とすることで実現できます。
この理論を応用することで、パーサーの互換性問題に対する形式的なアプローチが可能になります。
オートマトンを利用したパーサーの互換性の検証
パーサーとオートマトンを対応させる考え方は非常にシンプルです:
「パーサーpでコードwを正常にパースできる」<=>「オートマトンApが文字列wを受理する」
この対応関係を利用すると、2つのパーサーに対応するオートマトンを手に入れることができれば、それらが受理する言語の対称差(XOR)を計算することで互換性を検証できます。 対称差が空集合であれば、2つのパーサーは完全に互換性があると言えます。 逆に、対称差に含まれる文字列があれば、それは一方のパーサーでは正常にパースされるが、もう一方ではパースできずに構文エラーとなるコードの例となります。
この考え方を用いると、パーサーの互換性検証の基本的なアプローチは以下のように整理できます。
- 各パーサーに対応するオートマトンを定義する
- 両者が受理する言語の対称差を計算する
ここで問題となるのは、どうやってパーサーに対応するオートマトンを得るか?です。そこで登場するのが「オートマトン学習」という技術です。
オートマトン学習
オートマトン学習(automata learning)とは、中身のわからないブラックボックスのシステムからオートマトンを推測する技術です。本セッションでは、AngluinのL*というアルゴリズムが紹介されました。
L*はactive automata learningの一種で、アルゴリズム自体が自発的に質問(クエリ)を生成し、その回答から学習を進めていきます。L*では、以下の2種類の教師クエリを使用します:
Membership Query(MQ):
- 「この文字列はシステムで受理されますか?」という質問
- パーサーの場合、「このコードは正常にパースできますか?」という質問になる
Equivalence Query(EQ):
- 学習の最終段階で使用
- 「獲得したオートマトンはシステムと等価ですか?」という質問
- 等価でない場合は反例が返される
L*の学習プロセスは以下のようになります:
- Membership Queryを繰り返し、システムの挙動に関する情報を収集
- 収集した情報から仮のオートマトンを構築
- Equivalence Queryで構築したオートマトンの正確さを検証
- 間違いがあれば反例を基に学習を継続
ここで生じる疑問として、「プログラミング言語は正規表現で表現できるのか?」というものがあります。
形式言語を生成する形式文法の包含関係を示したチョムスキー階層では、正規表現は最も小さい集合、すなわち最も表現力が制限された文法とされています。
Rubyがどの言語クラスに属するのか正確にはわかっていませんが、少なくとも正規言語(正規表現によって記述される言語)の範囲を超えており、おそらく文脈自由言語に属するであろうと推測されています。
文脈自由言語は正規言語の範囲を超えた言語クラスですから、正規表現と同等の表現力しか持たないDFA、及びそれを利用した L*アルゴリズムでは学習に不十分であることが分かります。
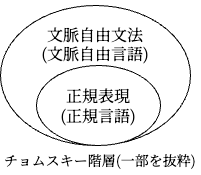
この制限を克服するために、DFAの代わりにより表現力の高い拡張されたオートマトンを用いる手法があります。
拡張されたオートマトンの例として、MDP(Markov Decision Process)、Symbolic Automata、Register Automaton、そしてVisibly Pushdown Automaton(VPA)などが挙げられます。 この中でVPAが重要です。 VPAは制限されたプッシュダウンオートマトンで、文脈自由言語の全てを扱えるわけではありませんが、括弧の対応などの重要な構文要素は扱えるという特徴があります。 Rubyの全文法は学習できないものの、部分的な構文パターンの学習には有効です。
VPAを用いることによって、より複雑な言語パターンも学習可能になり、パーサーの互換性検証に応用できるようになります。
lernen
本セッションでは、lernenという、makenowjustさんがRubyで実装したオートマトン学習のライブラリが紹介されました。
lernenは様々なオートマトン学習アルゴリズムに対応し、複数種類のオートマトンをサポートしています。
また、ユーザーフレンドリーなインターフェースとLernen.learnのような簡潔なAPIを提供し、Mermaid記法を用いたオートマトンの視覚化機能も備えています。
実際の応用例として、Rubyのパーサー互換性検証が紹介されました。
Rubyパーサー全体を学習するのは困難なため、使用する文字を4種類((, ), "a", :)に制限して実験が行われました。
この制限された範囲内でも、parse.yとPrismの間の互換性の問題を発見することに成功しました。
具体的には、("a":)というコードがPrismではシンボルとしてパースされるが、parse.yでは異なる解釈をするという問題が見つかりました(ruby/prism#3035)。このような微妙な違いは、通常のテスト手法では発見が難しいケースです。
lernenは、正規表現を使ったプログラムを別の実装に書き換える際の等価性チェックなどの場面で活用できます。例えば、正規表現の最適化や高速化の実装が元の正規表現と同じ挙動をするかを検証する際などに有用です。
実際にlernenを使ってみる
セッションの内容と直接関係ありませんが、実際にlernenを使ってオートマトン学習を試してみました。
lernenを使うときには、gemをインストールするだけで簡単に利用できます。
gem install lernen
今回は、メールアドレスのバリデーションを試しに実装してみて、それがRuby標準のライブラリにあるメールアドレス用の正規表現(URI::MailTo::EMAIL_REGEXP)と一致するかを確かめました。
まずは、以下のメールアドレスの検証コードを書いてみました。(以下のコードは間違っています!)
# 適当に書いた手書きのメールアドレスバリデーション def email_valid?(email) return false if email.nil? || email.empty? # ただ1つの@が含まれているか return false unless email.count('@') == 1 username, domain = email.split('@', 2) # ユーザー名が空でないか return false if username.empty? # ドメイン部分をドットで分割 domain_parts = domain.split('.') # ドメイン部分が空でないか return false if domain_parts.empty? domain_parts.each do |part| return false if part.empty? end true end
続いて、このメソッドがtrueを返す文字列と、URI::MailTo::EMAIL_REGEXPにマッチする文字列が等価であるかをlernenを使って検証してみました。
# frozen_string_literal: true require 'lernen' require 'uri' # アルファベットを定義する # a, b, 1, 2, @, . の6文字を使用 alphabet = %w[a b 1 2 @ .] # Oracle(Equivalence Queryのときに用いるテストケース)を定義する oracle = :random_word # アルファベットのランダムな組み合わせを利用する oracle_params = { max_words: 1000 }.freeze # `Lernen.learn`メソッドを使用して、DFAを学習する regex_dfa = Lernen.learn(alphabet:, oracle:, oracle_params:) do |word| # 標準ライブラリのメールアドレスの正規表現を使用する URI::MailTo::EMAIL_REGEXP.match?(word.join) end validator_by_hand_dfa = Lernen.learn(alphabet:, oracle:, oracle_params:) do |word| # 手書きのメールアドレスバリデーションを使用する email_valid?(word.join) end # 2つのDFAの対称差を計算し、片方では受理されるがもう片方では受理されない文字列を見つける sep_word = Lernen::Automaton::DFA.find_separating_word(alphabet, regex_dfa, validator_by_hand_dfa) if sep_word.nil? puts "✓ The two implementations are equivalent for our alphabet!" else test_case = sep_word.join puts "! Found a difference between implementations" puts " Test case: '#{test_case}'" puts " Regex implementation result: #{URI::MailTo::EMAIL_REGEXP.match?(test_case)}" puts " String ops implementation result: #{email_valid?(test_case)}" end # Mermaid記法で2つのDFAを出力 File.write("regex_email_dfa.mmd", regex_dfa.to_mermaid) File.write("validator_by_hand_dfa.mmd", validator_by_hand_dfa.to_mermaid)
このコードを実行して、以下の結果が得られました。
結果から、自分で実装したメールアドレスのバリデーションメソッドにはバグがあり、a@a.のようなドメイン部分の末尾にドットが来るケースも有効なメールアドレスであると判定してしまうことを発見できました。
$ ruby email_validator_example.rb ! Found a difference between implementations Test case: 'a@a.' Regex implementation result: false String ops implementation result: true
また、実際に学習されたDFAの様子がMermaid記法で得られ、以下のように視覚的に結果を確認することもできました。(すごい)
以下がURI::MailTo::EMAIL_REGEXPを教師として学習したDFAです。
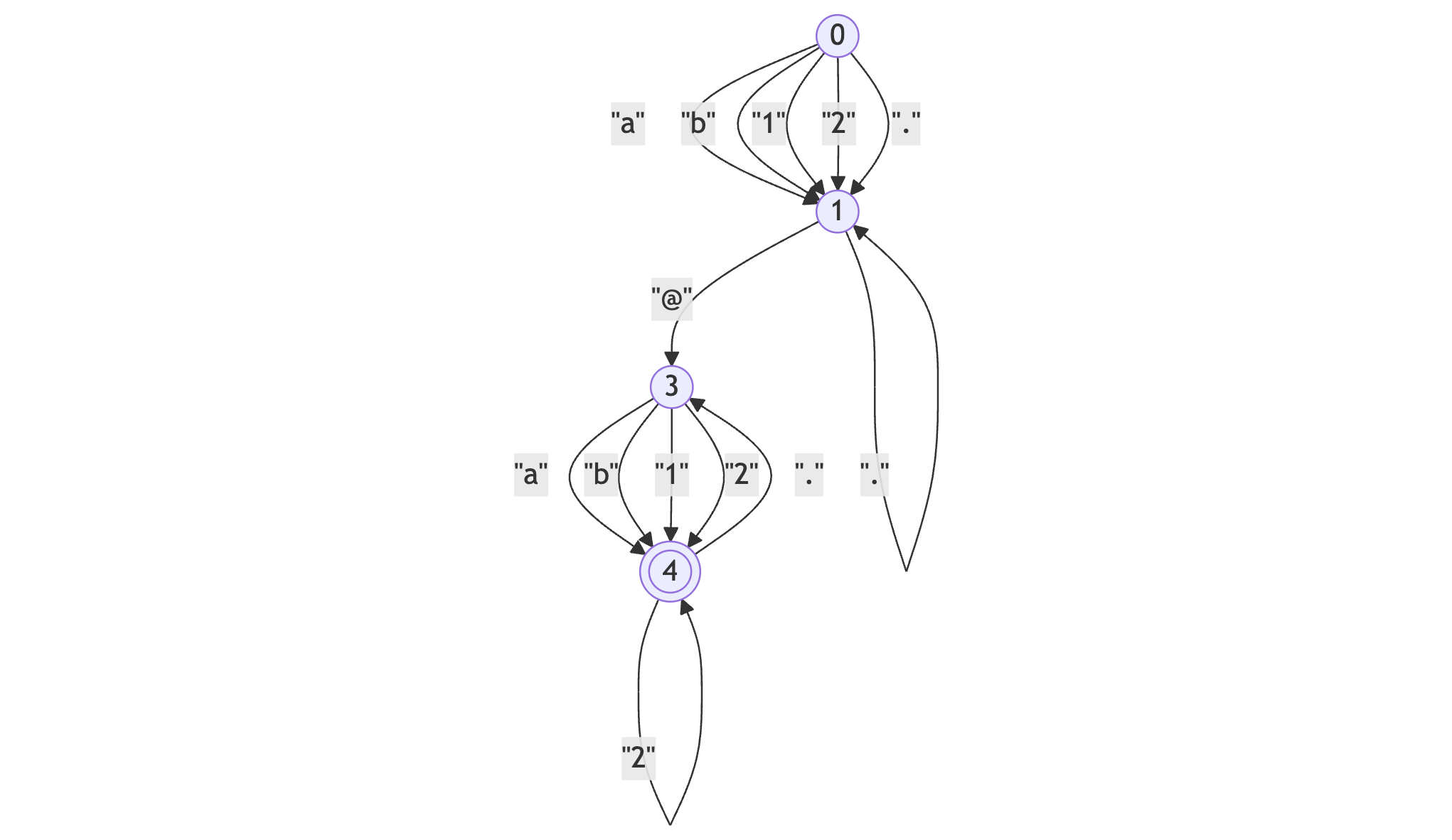
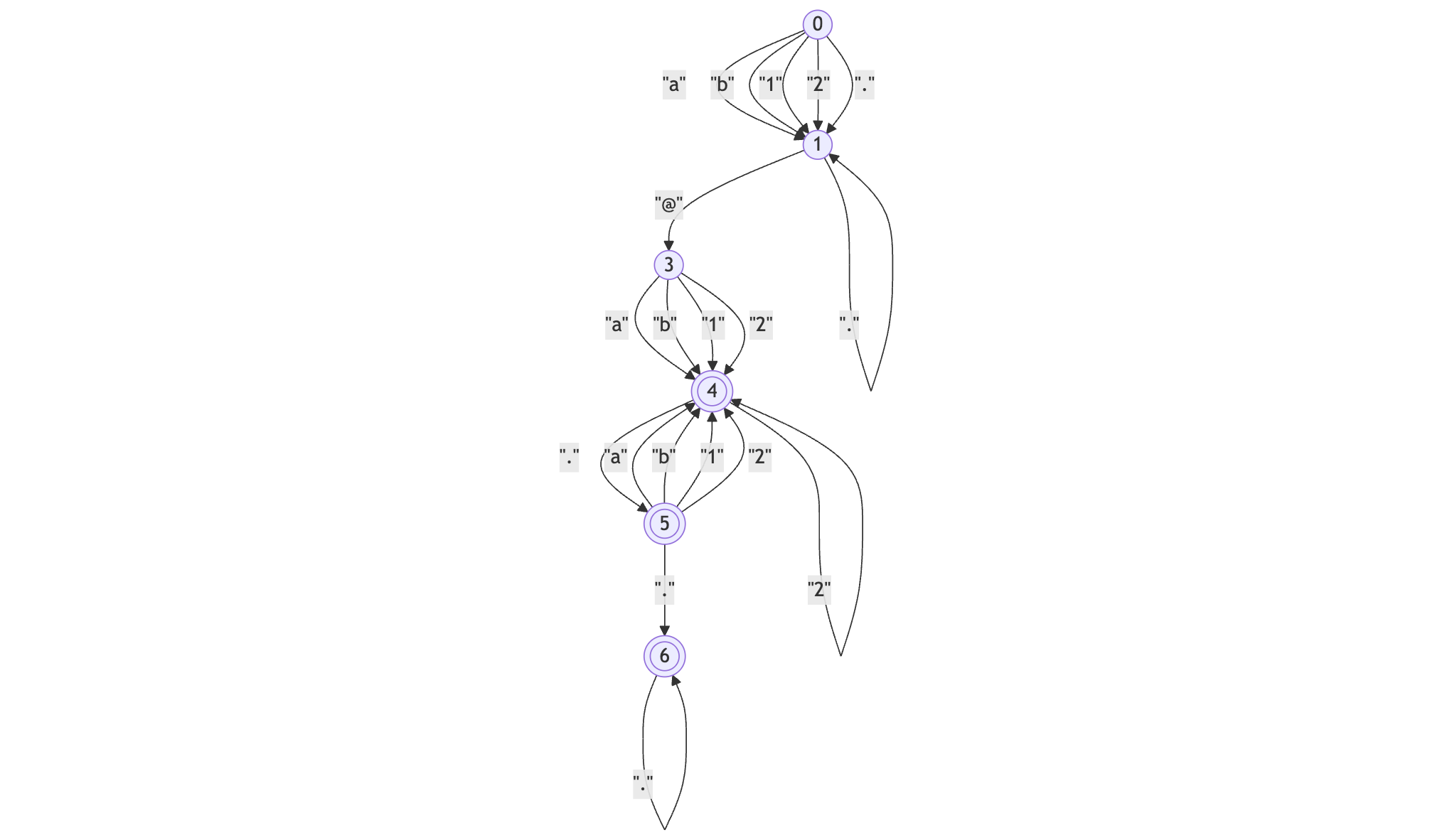
また、以下が手書きのメールアドレスのバリデーションを教師として学習したDFAです。
Future Work
セッションの最後には、今後の課題と展望について議論されました。
完全なパーサーの学習は依然として大きな課題です。その理由としては、まず学習対象のパーサーの複雑さが挙げられます。Rubyの構文は非常に複雑で文脈依存の要素も多くあります。 例を挙げると、まず以下のコードは構文エラーとなります。
foo /1
しかし、事前にfooが変数として定義されている以下の場合は、構文エラーとなりません。
foo = 1 foo /1
次に、計算量の問題があります。 L*アルゴリズムの計算量は、アルファベットのサイズをk、オートマトンの状態数をnとすると、O(kn²) と表されます。 実際のパーサーをオートマトンで表現するためには、膨大な数の状態が必要となるため、現実的な時間で学習を完了させるのは困難です。
さらに言語の特性として、Rubyの構文は正規言語の範囲を超えており、完全な学習は理論的にも難しいという課題があります。 しかし、部分的な構文パターンや特定の機能に焦点を当てた検証は十分に実用的です。 実際、本セッションでも制限された範囲内でパーサー間の互換性問題を発見することに成功しています。
また、本セッションでは、パース可能か否かに焦点を当てた検証をしましたが、最終的に重要なのは出力される構文木が一致することです。パースした結果に焦点を当てた互換性の検証も将来の課題として挙げられていました。
まとめ
本セッションでは、オートマトン学習という理論的なアプローチを用いて、Rubyの2つのパーサー(parse.yとPrism)間の互換性問題を検証する手法が紹介されました。
オートマトン理論とL*アルゴリズムを応用することで、従来のテスト手法では発見が難しかった微妙な互換性の問題を効率的に検出できることが示されました。特に、("a":)のような特定のコードパターンにおける解釈の違いを発見できたことは、この手法の有効性を示しています。
感想としては、オートマトン理論や形式言語理論といった大学の授業で習うような形式的・抽象的概念が、現実世界の問題解決に応用されている点が大変興味深く感じました。
RubyKaigiへの参加は初めてでしたが、このセッションの他にも多くの興味深いセッションがあり、とても貴重な経験となりました!
Techouseでは、社会課題の解決に一緒に取り組むエンジニアを募集しております。 ご応募お待ちしております。